The Physics of Thermal Inertia in Low-Slope Roof Design

What are the key material properties?

In a previous article the use of thermal inertia to slow down heat flux through a roof assembly was discussed. In buildings where air conditioning costs dominate and heating use is relatively low, higher thermal inertia assemblies can potentially improve energy efficiency. This is particularly the case of buildings such as offices that are only occupied during daylight hours. Thermal inertia could delay the transmission of heat into a building towards the end of the day, increasing thermal comfort and allowing facility managers to reduce cooling during the day.

While the previous article provided an introduction to thermal inertia and its potential benefits, it didn't discuss the origin of the property. Also, the related but different terms, thermal inertia and thermal mass, were used somewhat interchangeably.

This article describes the material properties that contribute to thermal inertia and provides a basis for material selection when increased thermal inertia is a goal.

Introduction

A building enclosure with high thermal inertia will slow down the transmission of heat. This effect has traditionally been used in the Mediterranean and other temperate climates to improve thermal comfort during the summer. As the building exterior surface heated up during the early afternoon period, high thermal inertia reduced the heat transmission into the interior. This was advantageous in the days before air conditioning. Today, designing with higher thermal inertia, as described in part one of this series, could improve energy efficiency in certain situations:

• Buildings located in areas where energy costs are dominated by air conditioning.
• Buildings only used during the day and not on a 24 hour basis. Thermal inertia can push heat loads into the evening, allowing for either temperature settings to be raised or HVAC fans speeds to be reduced.
• For high thermal inertia within the roof assembly to have a significant effect, low to moderate rise buildings with larger footprints would be best.

Thermal Inertia Effects

There are two key characteristics of thermal inertia; the decrement factor and time delay, both of which can be readily modeled and experimentally verified. A schematic showing these is shown below:

The time delay is calculated as:

Φ = t_[Tout(max)] - t_[Tin(max)]

Where t_[Tout(max)] and t_[Tin(max)] are the time of day when the inside and outside surface temperatures reach maximum. The decrement factor, DF, is calculated from:

DF = (T_in(max) – T_in(min)) / (T_out(max) – To_ut(min))

• The time delay and decrement factor could be used by building designers and operators to better optimize thermostat specification, HVAC use, and temperature schedules. As noted earlier, a large time delay could significantly reduce daily AC cooling demands for office buildings.
• Larger decrement factors can improve occupants' thermal comfort. Temperature swings are reduced, which in turn reduces HVAC cycling.
• Importantly, high thermal inertia will not reduce the energy reaching the interior, it only delays the transmission. This can make increased thermal inertia part of a strategy to improve energy efficiency in buildings occupied during the day but not necessarily for those occupied on a 24-hour basis.

Roof Configurations and Thermal Properties

Building designers and construction professionals are familiar with the property of thermal resistance, which is a measure of the extent to which a material blocks or resists heat transfer. It is expressed as R-value or U-value, which are numerical descriptions of the extent to which a material can resist heat flow.

However, there is far less familiarity with the time delay of heat transfer, or the extent to which a material slows down or delays heat transfer. As will be seen, a material can have low thermal resistance but still delay heat transfer. This is the crux of the underlying properties "thermal diffusivity", "thermal mass" and "thermal inertia".

Fundamental Thermo-Physical Properties

There are three fundamental thermo-physical properties of materials that are the components of thermal diffusivity, thermal inertia, and thermal mass. These are thermal conductivity, density, and specific heat capacity.

Thermal Conductivity

Building design professionals are very familiar with thermal conductivity, k, measured as watts per meter per Kelvin (W/(m.K)). It is normally used to characterize individual materials, for example polyiso foam, and is a measure of the heat flow through a material when a temperature gradient of 1K (i.e 1°C) is applied.

A related term, the u-factor, is used to describe the thermal conductivity of a system. This could be a window, i.e. a combination of glass, air space, and frame etc.

Thermal conductivity is measured when heat flow has equilibrated and it doesn't include any time delay.

Density

Density is a measure of the mass per unit volume, ρ=m/v. While this is straightforward for most materials, products such as polyiso can be harder to define. There are the facers and a small density gradient within the foam. Later, as values are listed, the facers will be ignored and the foam's density considered as an average.

Specific Heat Capacity

Specific heat capacity is defined as the amount of heat required to raise the temperature of 1 kilogram of a substance by 1 kelvin, or Cp = J/(kg.K). It is worth considering the simple diagram above, showing the measurement of thermal conductivity. At the onset, heat flow through the material is delayed by its specific heat capacity. It takes energy to raise its temperature, an action required before heat can then transmit.

Derived Thermo-Physical Properties

As noted, the fundamental properties described earlier are all measured at equilibrium and do not include any time lag or delay. For that, the following derived properties need to be considered.

Thermal Diffusivity

Thermal diffusivity is a measure of the rate at which a temperature propagates from one point to another point in a material. It's the rate of transfer of heat from a hot side to a cold side and is calculated as:

In a substance with high thermal diffusivity, heat moves rapidly through it because the substance conducts heat quickly relative to its volumetric heat capacity or 'thermal bulk'. In a sense, thermal diffusivity is what is meant when the topic of thermal inertia is discussed casually.

Thermal Inertia

Thermal inertia is the slowness with which the temperature of a material approaches that of its surroundings. It is a product of thermal conductivity, density, and specific heat capacity. From a building enclosure perspective, it could be considered as the rate at which the interior surface can supply heat into the interior, assuming a temperate climate.

It is arguable that thermal inertia is not the best property to use to characterize a building enclosure component in terms of thermal lag.

Thermal Mass

It is often broadly thought that thermal mass is essentially equivalent to gravimetric mass. Conceptually, this gives rise to the view that the more massive a construction the better. However, consider two blocks - one of steel and one of concrete - each having the same gravimetric mass. The two materials have different specific heat capacities and are not equivalent in terms of thermal properties. In addition, steel has a significantly higher thermal conductivity versus concrete.

Thermal mass is a property of a material that enables it to store heat and is the product of density and specific heat capacity:

Importantly, thermal mass doesn't fully describe thermal lag. High thermal mass would change the decrement factor, dampening out heat transmission but is only indirectly linked to thermal delay.

Roof Component Thermal Properties

Two deck types are predominant in North American construction of big-box type architecture; steel and concrete. Two possible idealized roof assemblies are shown below, based on the two roof deck types:

• Both systems have most roof assembly layers adhered. The steel deck system has a first layer of mechanically attached gypsum board to act as a substrate for the adhered first layer of polyiso.
• Thermal bridging is either minimal in the steel deck based system or absent in the concrete deck system (ignoring any real world penetrations).
• The first layer of gypsum board in the steel deck case could be used as a substrate for a vapor retarder.

The membrane, adhesive layers, and steel deck are relatively thin and have no significant insulating properties. The following table shows the fundamental and derived thermo-physical properties of the other components:

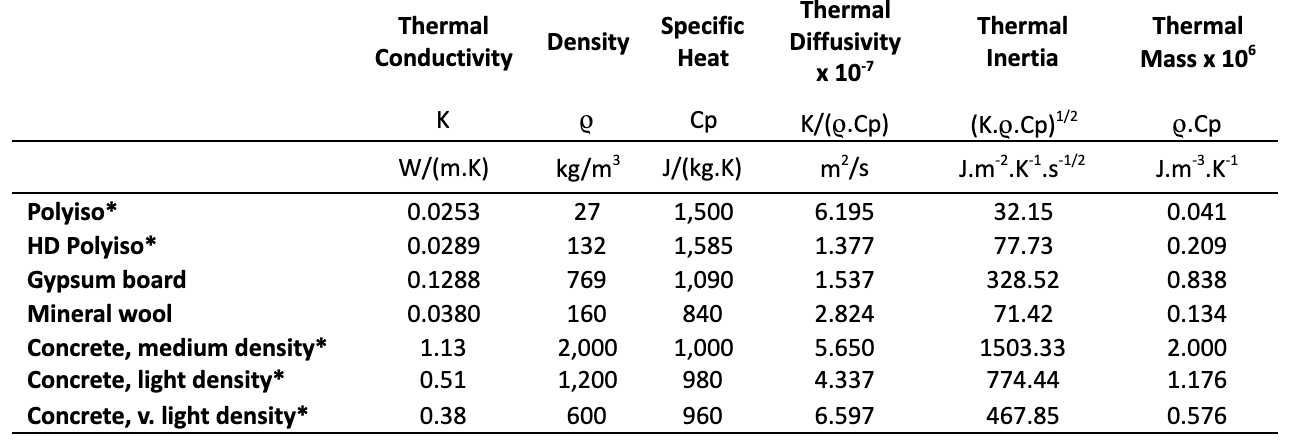
• Polyiso and HD Polyiso specific heat values are estimates.
• Concrete properties are very dependent on aggregate type and moisture level. Data shown represents average values for dry concrete.

Unsurprisingly, the data shows that concrete has significantly higher thermal mass and inertia versus the other materials compared in the table. As discussed in the first part of this series, insulation is best placed closest to the building exterior, and thermally massive materials placed closest to the interior. The southeast region tends to use concrete decks more than many other regions of the US, largely for improving the strength of the roof deck. This could also mean that, especially for those buildings occupied only during the day, such as offices, schools, and the like, have better opportunity for energy-efficiency benefits with well-designed roof insulation systems.

Conclusions

• Thermal property data could be used in modeling exercises to better understand how to design and optimize energy-efficient buildings.
• Clearly, concrete has a far higher thermal mass and inertia than other materials commonly used in roof assemblies.
• Very lightweight concrete and gypsum board have very similar thermal mass, thermal inertia, and density, but have notably different properties for thermal diffusivity and conductivity.

Thermal property data is fundamental to the materials used in low slope roof assemblies. However, it needs to be converted into values specific for the thickness and weight of actual roof products. That will be a topic for the next part of this series.

Sources Used

1. Verbeke, S., Thermal inertia in dwellings. Quantifying the relative effects of building thermal mass on energy use and overheating risk in a temperate climate. PhD Thesis, University of Antwerp, 2017.
2. Balaji, N. C., Mani, M., and Venkatarama, R. B. V., Thermal performance of building walls. 1st IBPSA Italy Conference, Building Simulation, 2013, pp. 151 – 159.